디지털 시대에서 정보 보안은 선택이 아닌 필수입니다. 우리가 매일 사용하는 스마트폰의 메시지, 온라인 뱅킹, SNS 인증, 이메일 암호화 등은 모두 복잡한 수학 정리를 기반으로 안전하게 보호되고 있습니다. 그 중심에는 RSA 암호 알고리즘과 이를 구성하는 핵심 수학 개념인 소수(prime number)와 모듈러 연산(modular arithmetic)이 있습니다.
이 글에서는 이러한 보안 시스템의 이론적 토대가 되는 수학 정리들을 자세히 소개합니다. 이 정리들은 단순한 수식이 아닌, 오늘날 세계를 움직이는 기술을 가능하게 한 수학적 기둥들입니다.
RSA 암호 시스템 – 공개키 암호화의 시작
개념 개요: RSA는 ‘공개키 암호화 방식’의 대표적 알고리즘으로, 데이터를 암호화할 때 하나의 키를 사용하고, 이를 해독할 때는 별도의 키를 사용하는 구조입니다. 즉, 암호화 키는 공개되어도 괜찮고, 복호화 키는 비밀로 유지됩니다.
원리:
- 두 개의 큰 소수 p, q를 선택하여 곱한 값 n = p × q를 생성합니다.
- 오일러 함수 φ(n) = (p−1)(q−1)를 구합니다.
- 1 < e < φ(n)인 정수 e를 공개키로 사용하며, e는 φ(n)과 서로소입니다.
- 개인키 d는 e × d ≡ 1 mod φ(n)을 만족하는 값으로 계산됩니다.
암호화와 복호화 공식:
- 암호화: C ≡ Me mod n
- 복호화: M ≡ Cd mod n
이 계산은 모듈러 지수 연산으로 처리되며, 해커가 C, e, n을 알아도 p와 q를 알지 못하면 d를 계산할 수 없습니다. 왜냐하면 n을 소인수분해하여 φ(n)을 얻는 것이 매우 어렵기 때문입니다.
중요한 점: 이 암호 체계의 안전성은 ‘큰 수의 소인수분해가 어렵다’는 수학적 사실에 기반합니다.
소수 – 암호 알고리즘의 뿌리
정의: 소수는 1과 자기 자신만을 약수로 가지는 자연수로, 정수론의 기본 구성 단위입니다. 모든 자연수는 유일한 소수의 곱으로 표현된다는 정수론의 기본 정리(Fundamental Theorem of Arithmetic)에 따라, 소수는 ‘수학의 원자’로 불립니다.
역사적 배경: 고대 그리스의 유클리드도 『기하원론』에서 소수의 무한성을 증명했으며, 오일러는 이후 합동식과 관련된 소수 정리를 확립했습니다. 현대에 와서는 대형 소수를 찾는 알고리즘이 개발되었으며, 2020년 기준으로 발견된 가장 큰 소수는 24,862,048자리입니다.
RSA와의 연결:
- 소수 p, q가 클수록 n = pq도 커지며 보안성이 높아집니다.
- 현재의 RSA는 보통 2048비트(약 617자리) 크기의 n을 사용합니다.
- 소수를 찾는 데는 밀러-라빈 테스트(Miller-Rabin Primality Test) 같은 고속 소수 판별법이 사용됩니다.
현대 기술 응용:
- 전자서명(Digital Signature Algorithm)
- HTTPS 인증서 기반의 브라우저 보안
- 블록체인 지갑 주소 생성과 전자지갑 키쌍 생성
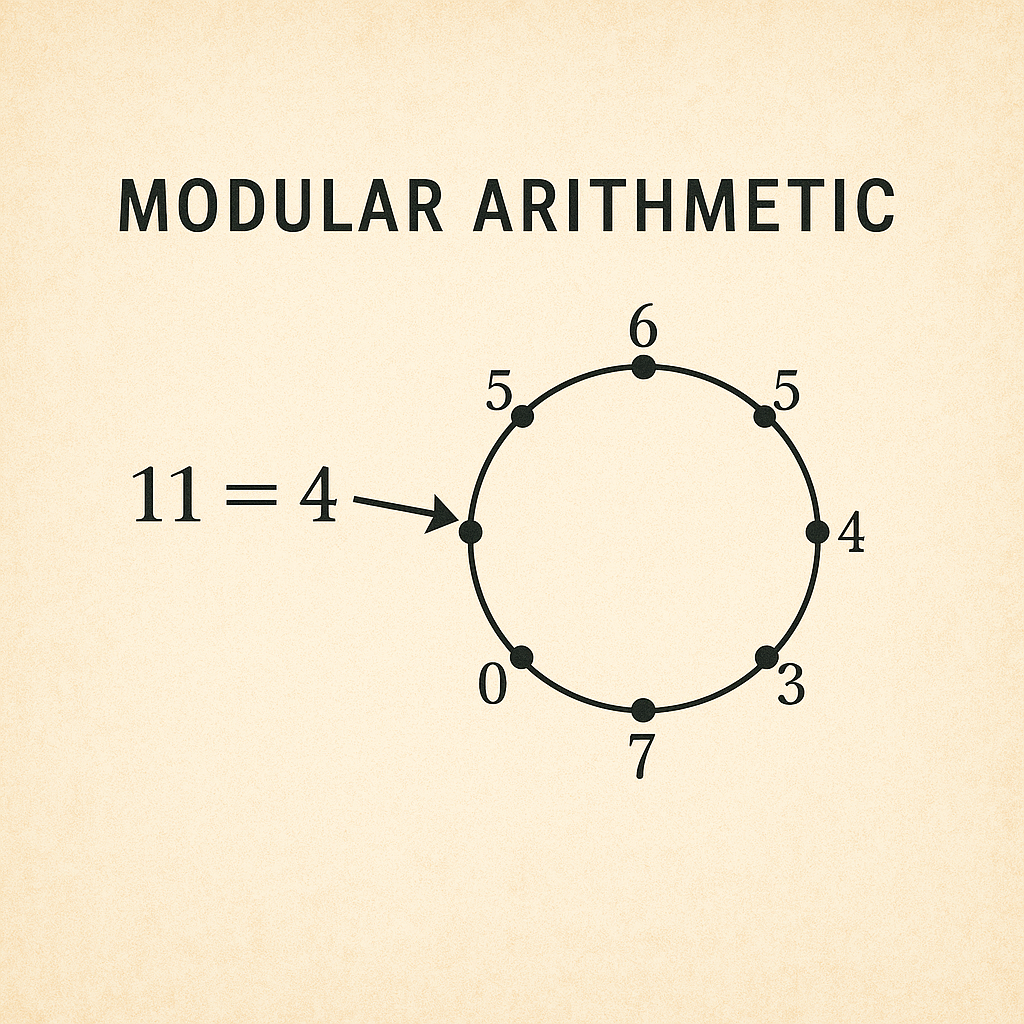
모듈러 연산 – 합동식으로 구현되는 수학 구조
정의: 모듈러 연산은 어떤 수를 정해진 수로 나눈 나머지를 구하는 연산입니다. 예: 13 mod 5 = 3 이 연산은 정수들의 집합을 순환 구조로 해석할 수 있게 해주며, 수학에서는 합동 관계 ≡로 표현합니다.
수학적 특징:
- a ≡ b mod n → a와 b를 n으로 나눈 나머지가 같다는 뜻
- 덧셈, 곱셈, 제곱 등 기본 연산이 모듈러 세계에서도 그대로 유지됨
- 지수 연산까지 확장 가능 (modular exponentiation)
암호와의 연결: RSA의 암호화와 복호화는 모두 모듈러 지수 연산에 기반하며, 암호 키 계산, 메시지 암호화 모두 ab mod n의 형태로 이루어집니다.
확장 응용 분야:
- 해시 함수 설계 (SHA-256 내부 연산)
- 비트코인 주소 생성, 트랜잭션 서명 (모듈러 곱셈 기반)
- 전자투표 시스템, 생체 인증 기반 키 교환 시스템
교육적 연결: 고등 수학에서 합동식은 수학 II 또는 심화 선택과목에서 배우며, 수리논술·정보올림피아드·코딩테스트 등에서도 자주 등장하는 주제입니다.
결론 – 수학 정리, 디지털 보안의 엔진
RSA 암호 시스템은 정수론의 정리들로 만들어졌습니다. 소수는 암호의 강도를, 모듈러 연산은 연산 효율성과 안전한 키 분배를 가능하게 합니다. 이 모든 구조는 수학 정리 위에 세워진 디지털 보안의 기둥입니다.
인터넷 쇼핑, 인터넷 뱅킹, 화상 회의, 비밀번호 보호 등 우리가 일상에서 누리는 수많은 디지털 기술 뒤에는 수학자들이 남긴 논리와 정리, 패턴과 예측이 숨어 있습니다.
암호학은 더 이상 군사 기술이나 해커의 세계에만 머무르지 않습니다. 이제 수학을 배우는 청소년, 개발자, 보안 엔지니어 모두가 알아야 할 기본 교양이 되었습니다.
수학 정리는 단순히 교과서 속의 공식이 아닙니다. 그것은 기술을 안전하게 만들고, 세계를 연결하며, 정보의 자유와 신뢰를 지켜주는 지적인 방패입니다.